Revisiting k-Means: 3 Approaches to Make It Work Higher
Picture by Writer | ChatGPT
Introduction
The k-means algorithm is a cornerstone of unsupervised machine studying, recognized for its simplicity and trusted for its effectivity in partitioning information right into a predetermined variety of clusters. Its simple strategy — assigning information factors to the closest centroid after which updating the centroid based mostly on the imply of the assigned factors — makes it one of many first algorithms most information scientists study. It’s a workhorse, able to offering fast and invaluable insights into the underlying construction of a dataset.
This simplicity comes with a set of limitations, nevertheless. Customary k-means typically struggles when confronted with the complexities of real-world information. Its efficiency may be delicate to the preliminary placement of centroids, it requires the variety of clusters to be specified prematurely, and it basically assumes that clusters are spherical and evenly sized. These assumptions not often maintain true within the wild, resulting in suboptimal and even deceptive outcomes.
Fortuitously, over the numerous years that k-means has been relied upon, the information science group has developed a number of intelligent modifications and extensions to deal with these shortcomings. These one-time hacks, however now core extensions, improve the robustness and applicability of k-means, reworking it from a easy textbook algorithm right into a instrument for sensible information evaluation.
This tutorial will discover three of the simplest methods to make k-means work higher within the wild, particularly:
Utilizing k-means++ for smarter centroid initialization
Leveraging the silhouette rating to seek out the optimum variety of clusters
Making use of the kernel trick to deal with non-spherical information
Let’s get began.
1. Smarter Centroid Initialization with k-means++
One of many biggest weaknesses of the usual k-means algorithm is its reliance on random centroid initialization. A poor preliminary placement of centroids can result in a number of issues, together with converging to a suboptimal clustering answer and requiring extra iterations to realize convergence, which then will increase computation time. Think about a state of affairs the place all preliminary centroids are randomly positioned inside a single, dense area of information — the algorithm may battle to accurately establish distinct clusters situated additional away. This sensitivity signifies that working the identical k-means algorithm on the identical information can produce completely different outcomes every time, making the method much less dependable.
The k-means++ algorithm was launched to beat this. As a substitute of purely random placement, k-means++ makes use of a better, nonetheless probabilistic methodology to seed the preliminary centroids. The method begins by selecting the primary centroid randomly from the information factors. Then, for every subsequent centroid, it selects a knowledge level with a likelihood proportional to its squared distance from the closest current centroid. This process inherently favors factors which can be additional away from the already chosen facilities, resulting in a extra dispersed and strategic preliminary placement. This strategy will increase the chance of discovering a greater last clustering answer and infrequently reduces the variety of iterations wanted for convergence.
Implementing this in apply is remarkably easy, as most trendy machine studying libraries — together with Scikit-learn — have built-in k-means++ because the default initialization methodology. By merely specifying init=”k-means++”, you possibly can leverage this approaches with none complicated coding.
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# Generate pattern information
X, y = make_blobs(n_samples=10000,
n_features=10,
facilities=5,
cluster_std=2.0,
random_state=42)
# Customary k-means with k-means++ initialization
kmeans_plus = KMeans(n_clusters=5, init=”k-means++”, n_init=1, random_state=42)
kmeans_plus.match(X)
# For comparability, normal k-means with random initialization
kmeans_random = KMeans(n_clusters=5, init=”random”, n_init=1, random_state=42)
kmeans_random.match(X)
print(f”k-means++ inertia: {kmeans_plus.inertia_}”)
print(f”Random initialization inertia: {kmeans_random.inertia_}”)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# Generate pattern information
X, y = make_blobs(n_samples=10000,
n_features=10,
facilities=5,
cluster_std=2.0,
random_state=42)
# Customary k-means with k-means++ initialization
kmeans_plus = KMeans(n_clusters=5, init=‘k-means++’, n_init=1, random_state=42)
kmeans_plus.match(X)
# For comparability, normal k-means with random initialization
kmeans_random = KMeans(n_clusters=5, init=‘random’, n_init=1, random_state=42)
kmeans_random.match(X)
print(f“k-means++ inertia: {kmeans_plus.inertia_}”)
print(f“Random initialization inertia: {kmeans_random.inertia_}”)
Output:
k-means++ inertia: 400582.2443257831
Random initialization inertia: 664535.6265023422
ok–means++ inertia: 400582.2443257831
Random initialization inertia: 664535.6265023422
As indicated by the variations in inertia — the sum of squared distances of information factors to their centroid — k-means++ outperforms random initialization considerably on this case.
2. Discovering the Optimum Variety of Clusters with the Silhouette Rating
An apparent limiting problem with k-means is the requirement that you simply to specify the variety of clusters, ok, earlier than working the algorithm. In lots of real-world situations, the optimum variety of clusters is just not recognized forward of time. Selecting an incorrect ok can result in both over-segmenting the information into meaningless micro-clusters or under-segmenting it by grouping distinct patterns collectively. Whereas strategies to assist decide the optimum variety of clusters just like the “elbow methodology” exist, they are often ambiguous and troublesome to interpret, particularly when there isn’t a transparent “elbow” within the visible plot of variance.
A extra sturdy and quantitative strategy is to make use of the silhouette rating. This metric gives a technique to consider the standard of a given clustering answer by measuring how well-separated the clusters are. For every information level, the silhouette rating is calculated based mostly on two values:
cohesion – the common distance to different factors in the identical cluster
separation – and the common distance to factors within the nearest neighboring cluster
Basically, we’re measuring how related information factors are to different information factors in their very own cluster, and the way completely different they’re from information factors in different clusters, which, intuitively, are precisely what a profitable k-means clustering answer must be maximizing.
Theese scores vary from -1 to +1, the place a excessive worth signifies that the purpose is well-matched to its personal cluster and poorly matched to neighboring clusters.
To search out the optimum ok, you possibly can run the k-means algorithm for a variety of various ok values and calculate the common silhouette rating for every. The worth of ok that yields the very best common rating is often thought-about the only option. This methodology gives a extra data-driven technique to decide the variety of clusters, shifting past easy heuristics and enabling a extra assured choice.
Let’s see the outcomes of calculating the silhouette rating for a variety of ok values from 2 to 10 utilizing Scikit-learn, decide which worth is the most effective, and plotting the outcomes to match to those outcomes.
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# Generate pattern information
X, y = make_blobs(n_samples=10000,
n_features=10,
facilities=5,
cluster_std=2.0,
random_state=42)
# Decide optimum ok (from 2 to 10) utilizing silhouette rating
silhouette_scores = []
k_values = vary(2, 11)
for ok in k_values:
kmeans = KMeans(n_clusters=ok, init=”k-means++”, n_init=10, random_state=42)
kmeans.match(X)
rating = silhouette_score(X, kmeans.labels_)
silhouette_scores.append(rating)
print(f”For ok = {ok}, the silhouette rating is {rating:.4f}”)
# Discover the optimum ok and greatest rating
best_score = max(silhouette_scores)
optimal_k = k_values[silhouette_scores.index(best_score)]
# Output last outcomes
print(f”nThe optimum variety of clusters (ok) is: {optimal_k}”)
print(f”This was decided by the very best silhouette rating of: {best_score:.4f}”)
# Visualizing the outcomes
plt.determine(figsize=(10, 6))
plt.plot(k_values, silhouette_scores, marker=”o”)
plt.title(‘Silhouette Scores for Varied Numbers of Clusters’)
plt.xlabel(‘Variety of clusters (ok)’)
plt.ylabel(‘Silhouette rating’)
plt.xticks(k_values)
plt.grid(True)
plt.present()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# Generate pattern information
X, y = make_blobs(n_samples=10000,
n_features=10,
facilities=5,
cluster_std=2.0,
random_state=42)
# Decide optimum ok (from 2 to 10) utilizing silhouette rating
silhouette_scores = []
k_values = vary(2, 11)
for ok in k_values:
kmeans = KMeans(n_clusters=ok, init=‘k-means++’, n_init=10, random_state=42)
kmeans.match(X)
rating = silhouette_score(X, kmeans.labels_)
silhouette_scores.append(rating)
print(f“For ok = {ok}, the silhouette rating is {rating:.4f}”)
# Discover the optimum ok and greatest rating
best_score = max(silhouette_scores)
optimal_k = k_values[silhouette_scores.index(best_score)]
# Output last outcomes
print(f“nThe optimum variety of clusters (ok) is: {optimal_k}”)
print(f“This was decided by the very best silhouette rating of: {best_score:.4f}”)
# Visualizing the outcomes
plt.determine(figsize=(10, 6))
plt.plot(k_values, silhouette_scores, marker=‘o’)
plt.title(‘Silhouette Scores for Varied Numbers of Clusters’)
plt.xlabel(‘Variety of clusters (ok)’)
plt.ylabel(‘Silhouette rating’)
plt.xticks(k_values)
plt.grid(True)
plt.present()
Output:
For ok = 2, the silhouette rating is 0.4831
For ok = 3, the silhouette rating is 0.4658
For ok = 4, the silhouette rating is 0.5364
For ok = 5, the silhouette rating is 0.5508
For ok = 6, the silhouette rating is 0.4464
For ok = 7, the silhouette rating is 0.3545
For ok = 8, the silhouette rating is 0.2534
For ok = 9, the silhouette rating is 0.1606
For ok = 10, the silhouette rating is 0.0695
The optimum variety of clusters (ok) is: 5
This was decided by the very best silhouette rating of: 0.5508
For ok = 2, the silhouette rating is 0.4831
For ok = 3, the silhouette rating is 0.4658
For ok = 4, the silhouette rating is 0.5364
For ok = 5, the silhouette rating is 0.5508
For ok = 6, the silhouette rating is 0.4464
For ok = 7, the silhouette rating is 0.3545
For ok = 8, the silhouette rating is 0.2534
For ok = 9, the silhouette rating is 0.1606
For ok = 10, the silhouette rating is 0.0695
The optimum quantity of clusters (ok) is: 5
This was decided by the highest silhouette rating of: 0.5508
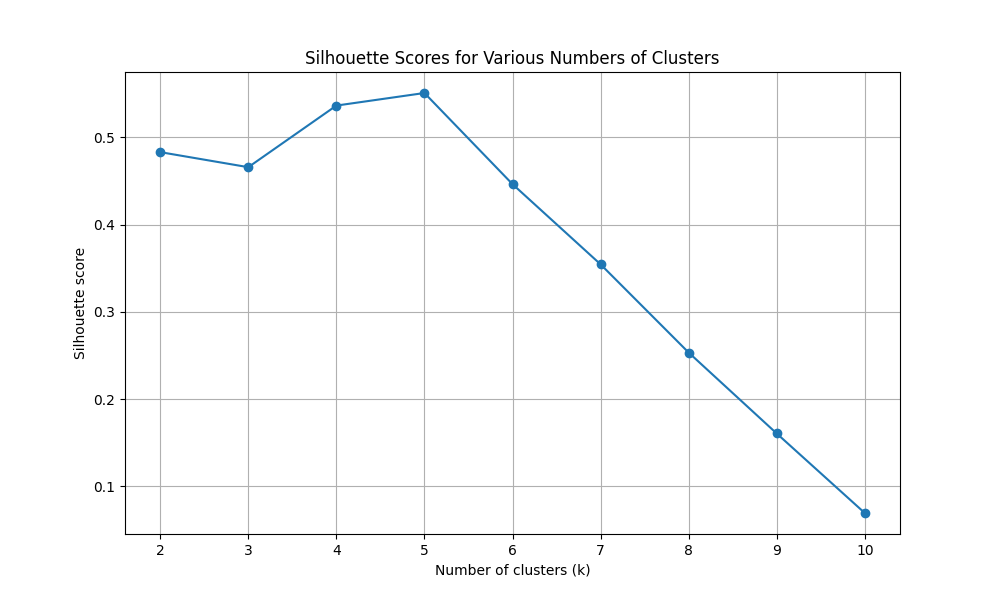
Determine 1: Silhouette scores for varied numbers of clusters (for ok values from 2 to 10)
We will see that 5 is the optimum ok worth with a silhouette rating of 0.5508.
3. Dealing with Non-Spherical Clusters with Kernel k-Means
Maybe essentially the most irritating and unrealistic limitations of k-means is its assumption that clusters are convex and isotropic, that means they’re roughly spherical and have related sizes. It is because k-means defines clusters based mostly on the space to a central level, which inherently creates sphere-like boundaries. When confronted with real-world information that comprises complicated, elongated, or non-linear shapes, normal k-means fails to establish these patterns accurately. For instance, it could be unable to separate two concentric rings of information factors, as it could possible break up them with a straight line.
To handle this, we will make use of the kernel trick, an idea central to the workings of assist vector machines. Kernel k-means works by implicitly projecting the information right into a higher-dimensional area the place the clusters might change into linearly separable or extra spherical. That is executed utilizing a kernel perform, such because the radial foundation perform (RBF), which computes the similarity between information factors on this higher-dimensional area with out ever having to explicitly calculate their new coordinates. By working on this reworked function area, kernel k-means can establish clusters with complicated, non-spherical shapes that may not be attainable for the usual algorithm to detect.
Whereas Scikit-learn doesn’t have a direct KernelKMeans implementation, its SpectralClustering algorithm gives a strong different that successfully achieves an identical consequence. Spectral clustering makes use of the connectivity of the information to type clusters and is especially efficient at discovering non-convex clusters. It may be seen as a type of kernel k-means and serves as a superb instrument for this goal. Let’s have a look.
from sklearn.cluster import KMeans, SpectralClustering
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
# Generate non-spherical information
X, y = make_moons(n_samples=500, noise=0.05, random_state=42)
# Visualize the non-spherical information
plt.determine(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], coloration=”blue”, s=15)
# Add titles and labels for readability
plt.title(‘Pattern Non-Spherical Information’)
plt.xlabel(‘Characteristic 1’)
plt.ylabel(‘Characteristic 2′)
plt.grid(True, linestyle=”–“, alpha=0.6)
plt.present()
# Apply normal k-means
kmeans = KMeans(n_clusters=2, n_init=10, random_state=42)
kmeans_labels = kmeans.fit_predict(X)
# Apply spectral clustering (in its place for kernel k-means)
spectral = SpectralClustering(n_clusters=2, affinity=’nearest_neighbors’, random_state=42)
spectral_labels = spectral.fit_predict(X)
# Visualizing the outcomes
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
ax1.scatter(X[:, 0], X[:, 1], c=kmeans_labels, cmap=’viridis’, s=50)
ax1.set_title(‘Customary Ok-Means Clustering’)
ax1.set_xlabel(‘Characteristic 1’)
ax1.set_ylabel(‘Characteristic 2′)
ax2.scatter(X[:, 0], X[:, 1], c=spectral_labels, cmap=’viridis’, s=50)
ax2.set_title(‘Spectral Clustering’)
ax2.set_xlabel(‘Characteristic 1’)
ax2.set_ylabel(‘Characteristic 2’)
plt.suptitle(‘Comparability of Clustering on Non-Spherical Information’)
plt.present()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
from sklearn.cluster import KMeans, SpectralClustering
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
# Generate non-spherical information
X, y = make_moons(n_samples=500, noise=0.05, random_state=42)
# Visualize the non-spherical information
plt.determine(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], coloration=‘blue’, s=15)
# Add titles and labels for readability
plt.title(‘Pattern Non-Spherical Information’)
plt.xlabel(‘Characteristic 1’)
plt.ylabel(‘Characteristic 2’)
plt.grid(True, linestyle=‘–‘, alpha=0.6)
plt.present()
# Apply normal k-means
kmeans = KMeans(n_clusters=2, n_init=10, random_state=42)
kmeans_labels = kmeans.fit_predict(X)
# Apply spectral clustering (in its place for kernel k-means)
spectral = SpectralClustering(n_clusters=2, affinity=‘nearest_neighbors’, random_state=42)
spectral_labels = spectral.fit_predict(X)
# Visualizing the outcomes
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
ax1.scatter(X[:, 0], X[:, 1], c=kmeans_labels, cmap=‘viridis’, s=50)
ax1.set_title(‘Customary Ok-Means Clustering’)
ax1.set_xlabel(‘Characteristic 1’)
ax1.set_ylabel(‘Characteristic 2’)
ax2.scatter(X[:, 0], X[:, 1], c=spectral_labels, cmap=‘viridis’, s=50)
ax2.set_title(‘Spectral Clustering’)
ax2.set_xlabel(‘Characteristic 1’)
ax2.set_ylabel(‘Characteristic 2’)
plt.suptitle(‘Comparability of Clustering on Non-Spherical Information’)
plt.present()
Output:
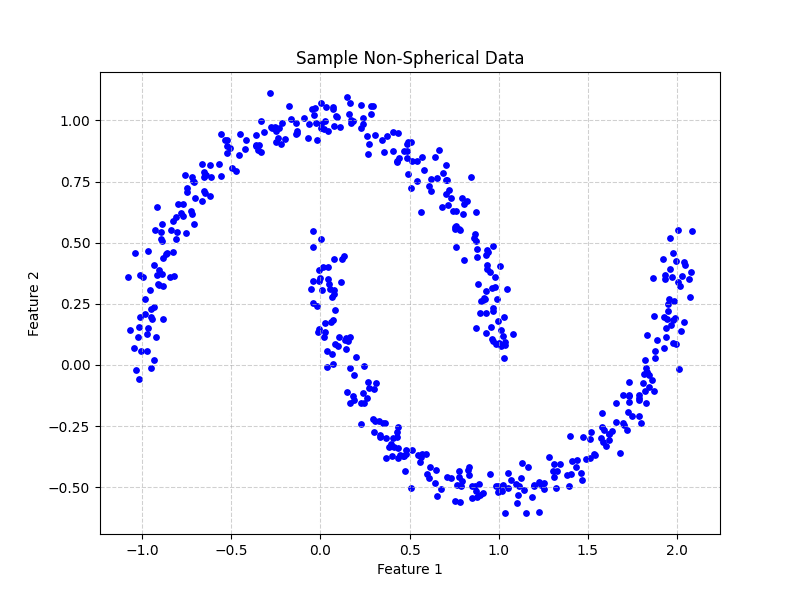
Determine 2: Pattern non-spherical information
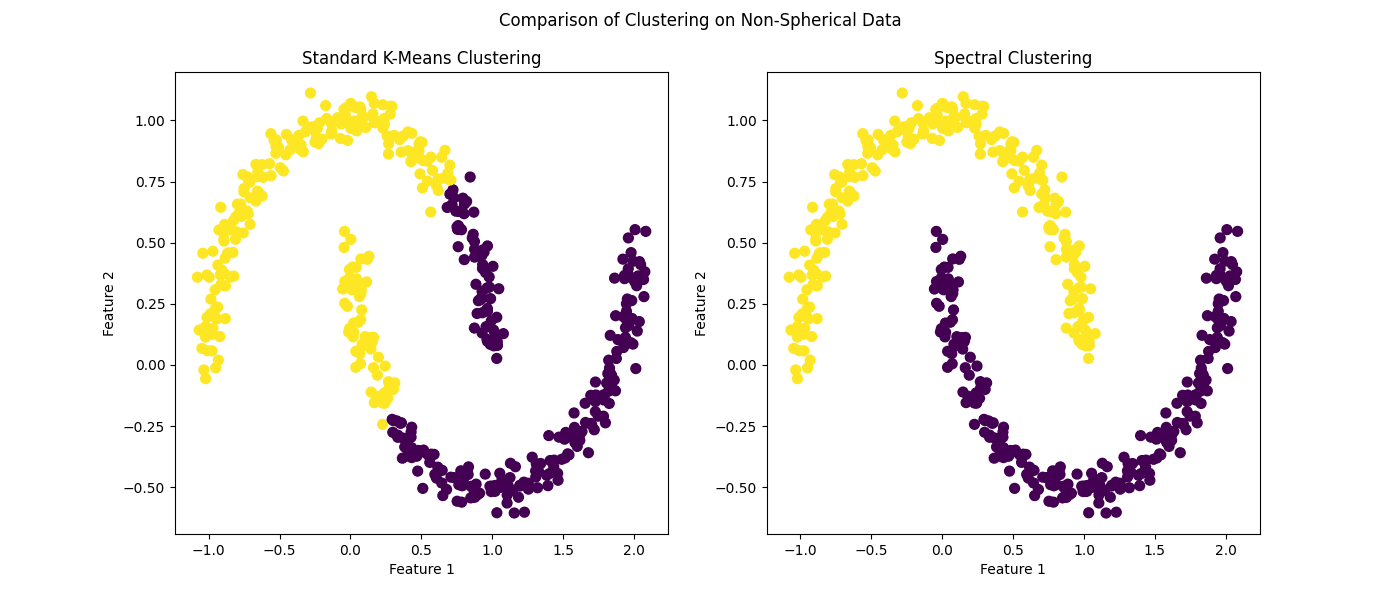
Determine 3: Comparability of clustering on non-spherical information
It hardly must be identified that spectral clustering — as a stand-in for kernel k-means — outperforms its normal counterpart on this state of affairs.
Wrapping Up
Whereas the k-means algorithm is commonly launched as a fundamental clustering method, its utility extends past introductory examples. By incorporating a number of intelligent approaches, we will overcome its most vital limitations and adapt it for the messy, complicated nature of real-world information. These enhancements show that even foundational algorithms can stay extremely related and highly effective with the precise modifications:
Utilizing k-means++ for initialization gives a extra sturdy place to begin, main to raised and extra constant outcomes.
The silhouette rating gives a quantitative methodology for figuring out the optimum variety of clusters, eradicating the guesswork from one of many algorithm’s key parameters.
Leveraging kernel strategies by way of methods like spectral clustering permits k-means to interrupt free from its assumption of spherical clusters and establish intricate patterns within the information.
Don’t be so fast to dismiss k-means; by making use of these sensible methods, you possibly can unlock its full potential and acquire deeper, extra correct insights out of your information.







